Calculs de puissance
Summary
Cette ressource décrit l’intuition qui sous-tend les calculs de puissance et fournit aux chercheurs des conseils pratiques et des exemples de code permettant d’effectuer ce type de calculs à l’aide de commandes intégrées ou de simulations. Elle suppose une certaine connaissance des statistiques et des tests d’hypothèse. Les lecteurs intéressés par des analyses plus techniques peuvent se référer aux liens qui figurent à la fin de cette ressource, tandis que ceux qui cherchent des exemples de code permettant d’effectuer des calculs de puissance sous Stata et sous R peuvent consulter les liens fournis dans la section « Exemples de code ». Si vous maîtrisez déjà l'intuition et les aspects techniques des calculs de puissance, vous pouvez vous référer à notre Petit guide des calculs de puissance.
Principes fondamentaux
- La capacité d’une expérimentation à détecter les différences entre le groupe de traitement et le groupe témoin est mesurée par la puissance statistique.
- Une erreur de type I est un faux positif : on rejette à tort l’hypothèse nulle selon laquelle il n’y a pas d’effet, ou on conclut, à tort, que l’intervention a eu un effet alors que ce n’est pas le cas. La probabilité de commettre une erreur de type I est exprimée par α.
- Une erreur de type II est un faux négatif : on ne détecte pas d’effet alors qu’il y en a un. La probabilité de commettre une erreur de type II est généralement donnée par β. Cependant, dans cette ressource, les erreurs de type II seront désignées par pour les différencier de l’effet du traitement β.
- La puissance est la probabilité de rejeter l’hypothèse nulle lorsque celle-ci est fausse. Formellement, la puissance est généralement exprimée par 1-β. Cependant, toujours pour la distinguer de l’effet du traitement β, la puissance sera désignée par 1- dans cette ressource. En d’autres termes, maximiser la puissance statistique revient à minimiser la probabilité de commettre une erreur de type II.
- Les calculs de puissance consistent soit à déterminer la taille d’échantillon nécessaire pour détecter l’effet minimum désiré compte tenu de plusieurs autres paramètres, soit à déterminer quelle taille d’effet l’étude sera en mesure de détecter pour une taille d’échantillon donnée et compte tenu de divers autres paramètres.
Le protocole de l’évaluation, le taux de participation au traitement et le taux d’attrition influent également sur la puissance, comme nous le verrons plus en détail par la suite.
Les calculs de puissance reposent notamment sur les paramètres suivants :
Le niveau de signification (α) : La probabilité de faire une erreur de type I. Il est généralement fixé à 5 %, soit α=0,05. La puissance du test (1-) : Elle est généralement fixée à 0,8, ce qui signifie que la probabilité de ne pas rejeter l’hypothèse nulle lorsqu’elle est fausse est de 0,2, ou 20 %. La puissance est étroitement liée au niveau de signification α : lorsque α augmente (passant par exemple de 1 % à 5 %), la probabilité de rejeter l’hypothèse nulle augmente, ce qui se traduit par un test plus puissant. L’effet minimum détectable (EMD, ou MDE en anglais) : Le plus petit effet qui, s’il est réel, a (1-) % de chance de produire une estimation statistiquement significative au seuil de α % (Bloom 1995). En d’autres termes, l’EMD correspond à la taille minimale d’effet en dessous de laquelle on risque de ne pas pouvoir repérer un effet différent de zéro, même s’il existe. La taille de l’échantillon (N) La variance de la variable d’intérêt (2) L’allocation du traitement (P) : La part de l’échantillon qui est allouée au groupe de traitement. Si c’est normalement la répartition égale des unités entre les différents bras expérimentaux qui permet de maximiser la puissance de l’étude, il existe toutefois quelques cas particuliers où l’on optera pour une répartition inégale. Le coefficient de corrélation intra-grappe (CCI, ou ICC en anglais) : Mesure de la corrélation entre les observations au sein d’une même grappe, souvent exprimée par ⍴. Si l’étude repose sur une randomisation en grappes (en d’autres termes, si chaque unité de randomisation contient plusieurs unités d’observation), il faut tenir compte du fait que les individus (ou les ménages, etc.) d’un même groupe, par exemple une ville, un village ou une école, sont plus semblables les uns aux autres que ceux qui appartiennent à des groupes différents1. Cela nécessite généralement une taille d’échantillon plus importante.
| Component | Relationship to power | Relationship to MDE |
| Sample size (N) increase | Increases power | Decreases the MDE |
| Outcome variance decrease | Increases power | Decreases the MDE |
| True effect size increases | Increases power | n/a |
| Equal treatment allocation (P) | Increases power | Decreases the MDE |
| ICC increases | Decreases power | Increases the MDE |
Introduction
Les tests d’hypothèse se concentrent sur la probabilité de commettre une erreur de type I, qui consiste à rejeter à tort l’hypothèse nulle selon laquelle 𝛃=0, c’est-à-dire de conclure à tort que le traitement a un effet alors qu’il n’en a pas. Comme indiqué ci-dessus, le niveau de signification est généralement fixé à 5 %. Cependant, en adoptant ce seuil conservateur, on augmente le risque de commettre un autre type d’erreur, à savoir une erreur de type II, qui consiste à ne détecter aucun effet alors que le traitement en a un. La puissance statistique se définit comme la probabilité de ne PAS commettre d’erreur de type II2. En d’autres termes, elle consiste à rejeter à raison l’hypothèse nulle lorsque le traitement a effectivement un effet, ou [1-prob(erreur de type II)].
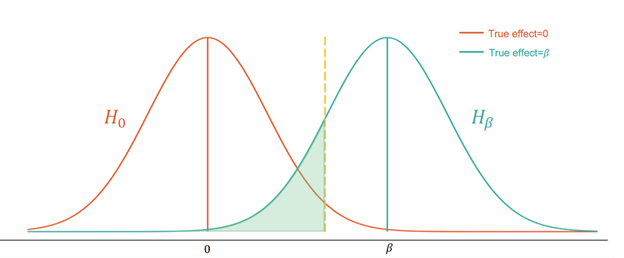
Le graphique ci-dessous montre comment une erreur de type II peut survenir :
Dans la Figure 1, la courbe orange représente la distribution de sous l’hypothèse nulle, et la courbe turquoise la distribution de sous l’hypothèse alternative. La zone ombrée en vert représente 20 % de la surface située sous la courbe turquoise. Si l’effet réel est 𝛽, la zone ombrée en vert représente la probabilité de ne pas rejeter l’hypothèse nulle alors que l’hypothèse alternative est vraie.
Dans la Figure 1, la courbe orange représente la distribution de sous l’hypothèse nulle, et la courbe turquoise la distribution de sous l’hypothèse alternative. La zone ombrée en vert représente 20 % de la surface située sous la courbe turquoise. Si l’effet réel est 𝛽, la zone ombrée en vert représente la probabilité de ne pas rejeter l’hypothèse nulle alors que l’hypothèse alternative est vraie.
Randomisation au niveau de l’unité d’observation
Équations pour calculer la puissance et la taille de l’échantillon
On distingue deux approches principales pour calculer la puissance, selon que la taille de l’échantillon est pré-déterminée ou non :
-
Si la taille de l’échantillon est pré-déterminée, que ce soit en raison de contraintes budgétaires ou de facteurs externes (par exemple, le nombre d’enfants éligibles dans les écoles du partenaire), les calculs de puissance permettent de déterminer quelle taille d’effet l’étude est en mesure de détecter (l’EMD, ou MDE en anglais). Les chercheurs décident alors si l’étude peut être mise en œuvre telle qu’elle a été conçue, ou si elle doit être modifiée afin d’en augmenter la puissance. De manière formelle3 :
- Si la taille de l’échantillon n’est pas pré-déterminée ni plafonnée à un niveau prédéfini, on peut effectuer des calculs de puissance pour identifier la taille minimale d’échantillon nécessaire pour détecter une taille d’effet donnée (l’EMD) compte tenu des différents paramètres :
Où, comme défini plus haut, N désigne la taille de l’échantillon, $\sigma^2$ la variance de la variable d’intérêt (supposée égale dans chaque bras de traitement), P l’allocation du traitement, et $t_{1-\kappa}$ et $t_{\frac{\alpha}{2}}$ les valeurs critiques d’une distribution t de Student pour la puissance et le niveau de signification, respectivement. Les protocoles plus complexes, notamment ceux qui incluent des grappes, des covariables ou des strates, nécessitent davantage d’informations (voir plus bas). Vous trouverez plus bas, dans la section « Conseils pratiques », des précisions sur les sources potentielles permettant d’obtenir ces informations.
Relation entre la puissance et les paramètres qui l’influencent
Les figures et les équations présentées dans la section précédente nous ont permis d’explorer plus en profondeur l’intuition qui sous-tend les relations entre la puissance et les paramètres qui l’influencent, toutes choses égales par ailleurs. Cette nouvelle section approfondit l’étude de ces différentes relations avant de les synthétiser dans un tableau récapitulatif.
Variance des variables d’intérêt et taille de l’échantillon
La variance des variables d’intérêt au sein de l’échantillon diminue à mesure que la taille de l’échantillon augmente, car les échantillons de plus grande taille sont plus représentatifs de la population de référence. Augmenter la taille de l’échantillon permet donc une estimation plus précise de l’effet du traitement, ce qui réduit la probabilité de commettre une erreur de type II et augmente la puissance de l’étude. Il en va de même pour les variables qui présentent une variance plus faible au sein de la population de référence, car la variance de l’échantillon est généralement moins importante lorsque la variance de la population l’est aussi. Notons que l’on peut arriver au même constat de façon analytique en utilisant le calcul des erreurs-types décrit plus haut : lorsque la taille de l’échantillon (N) augmente ou que la variance de la population (𝜎2) diminue, l’erreur-type diminue
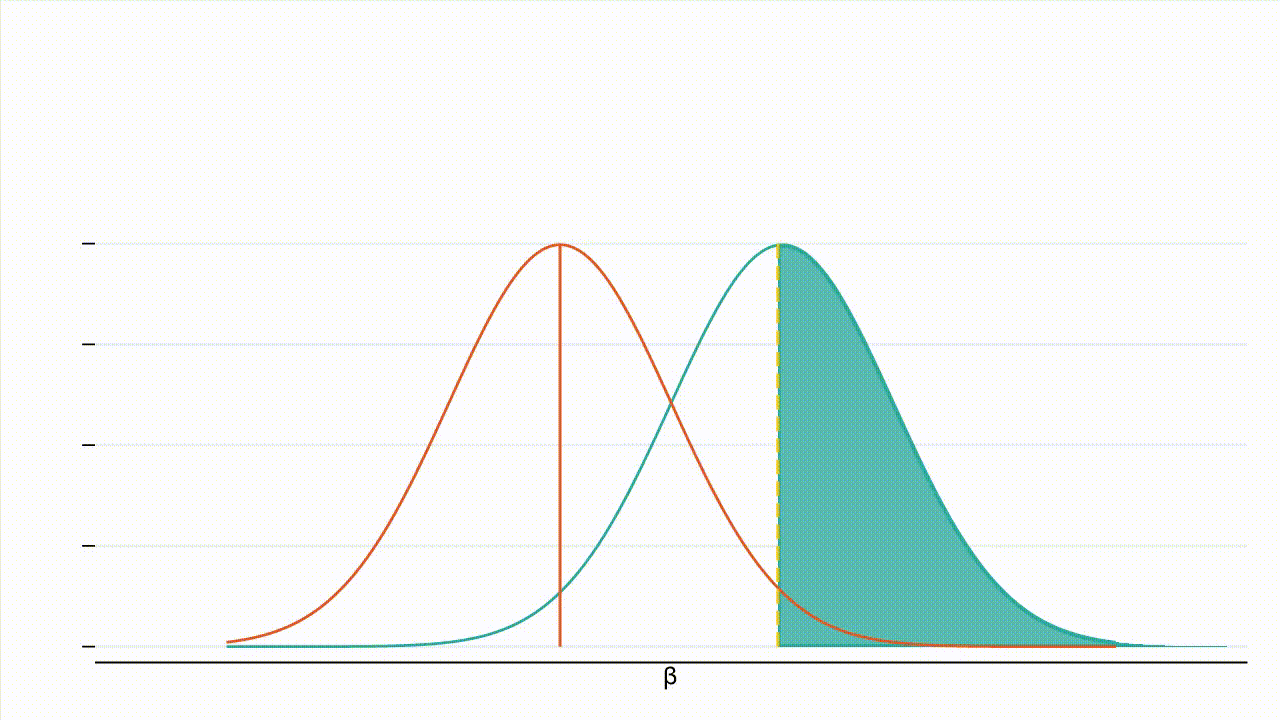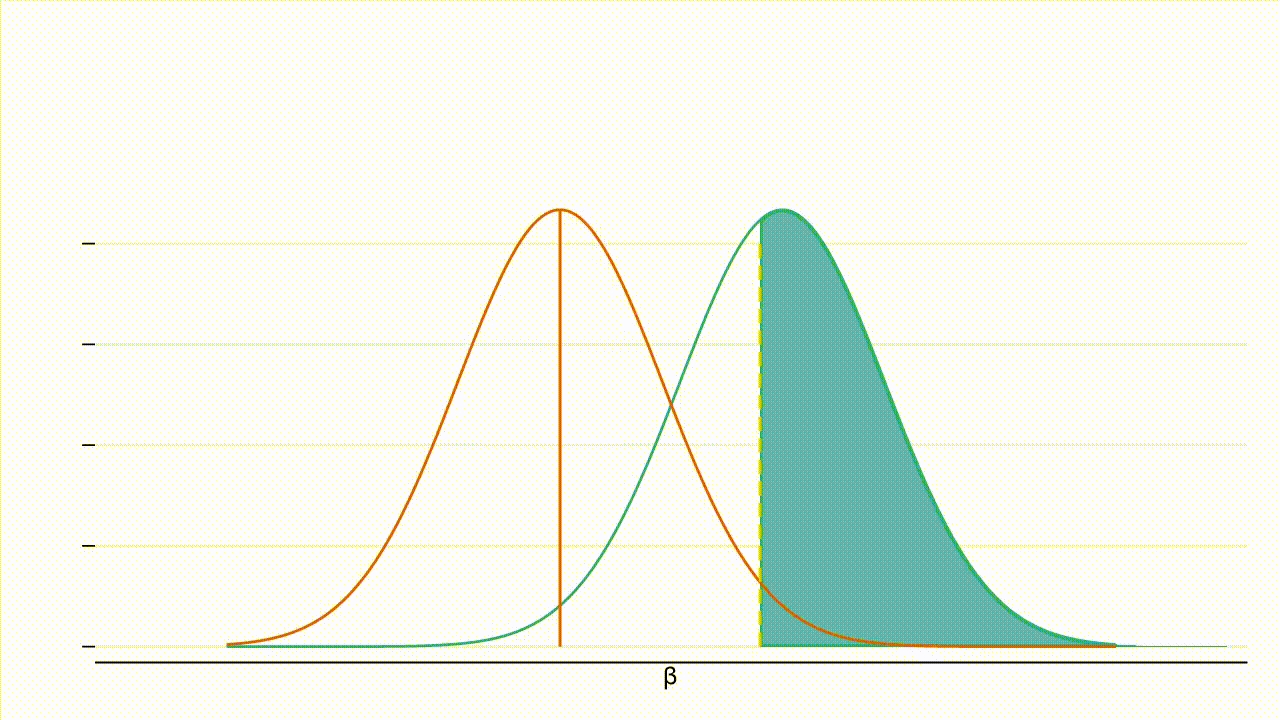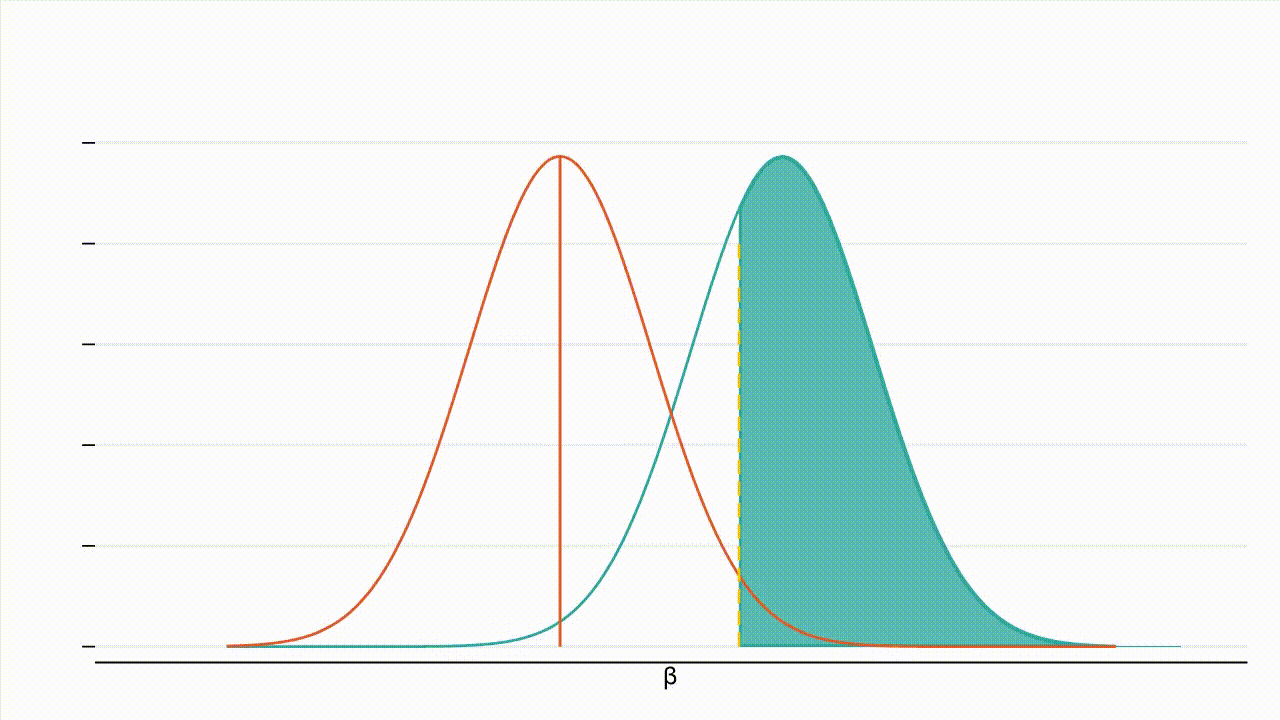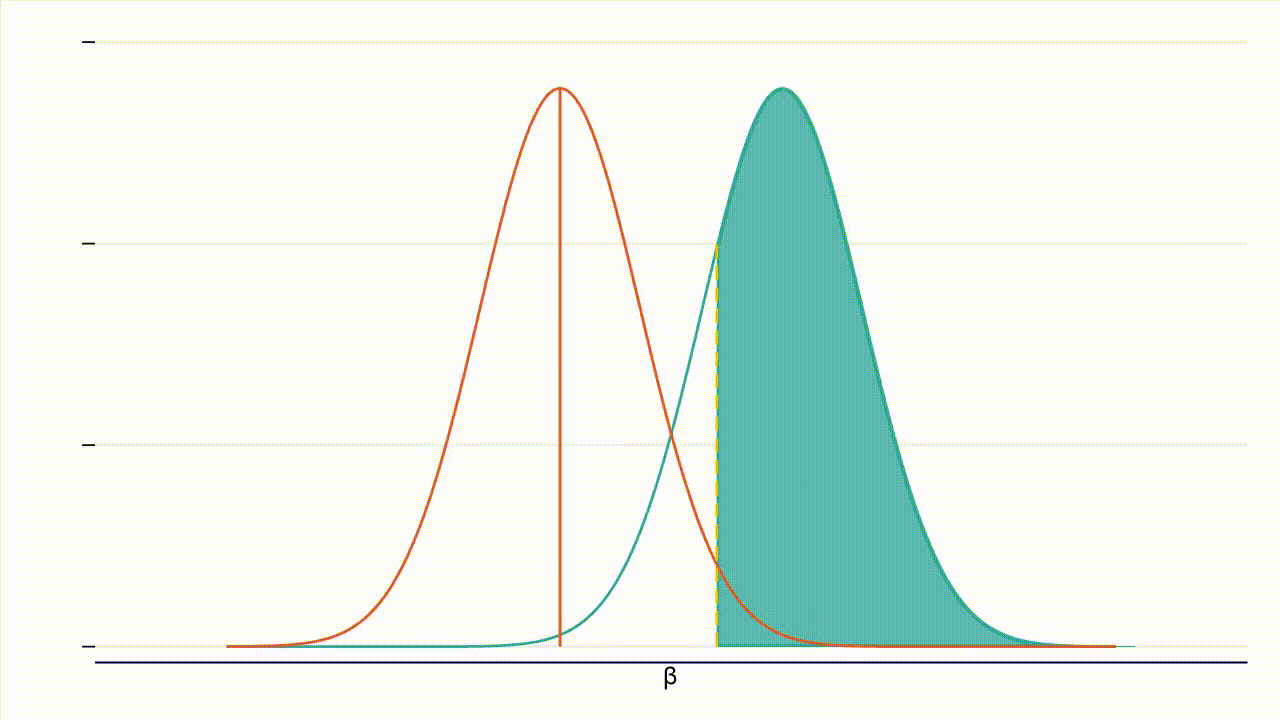
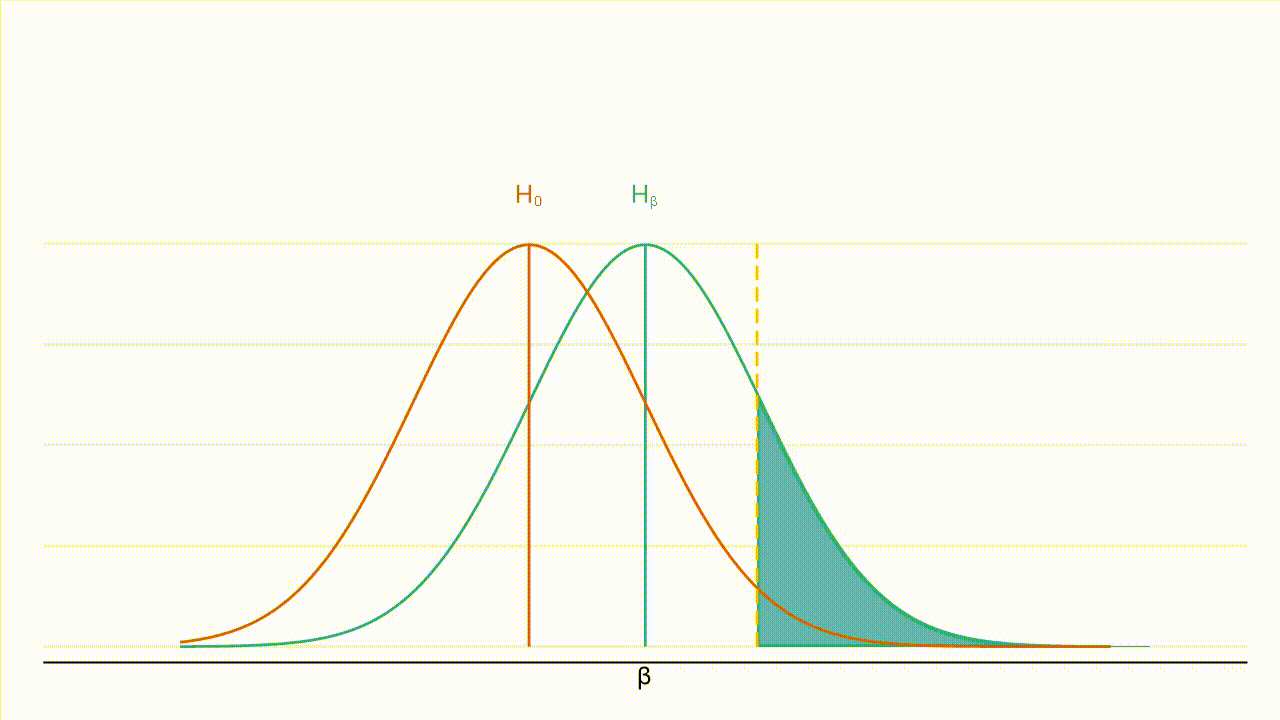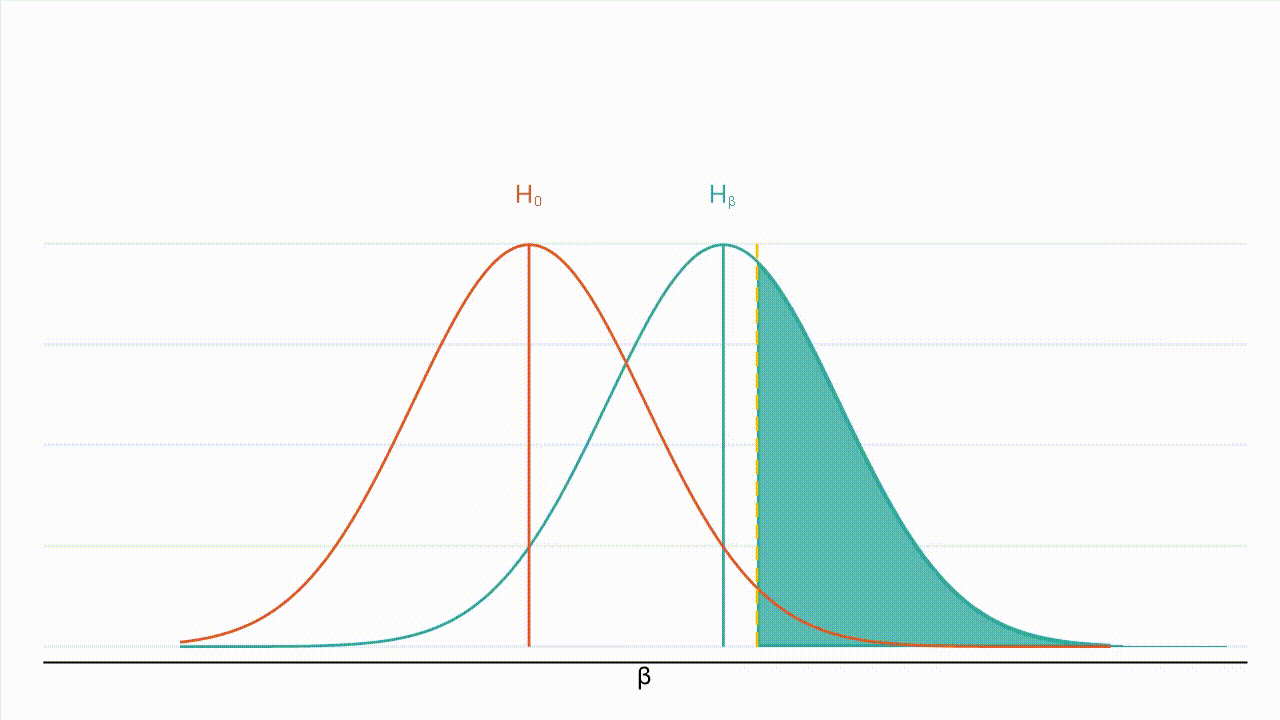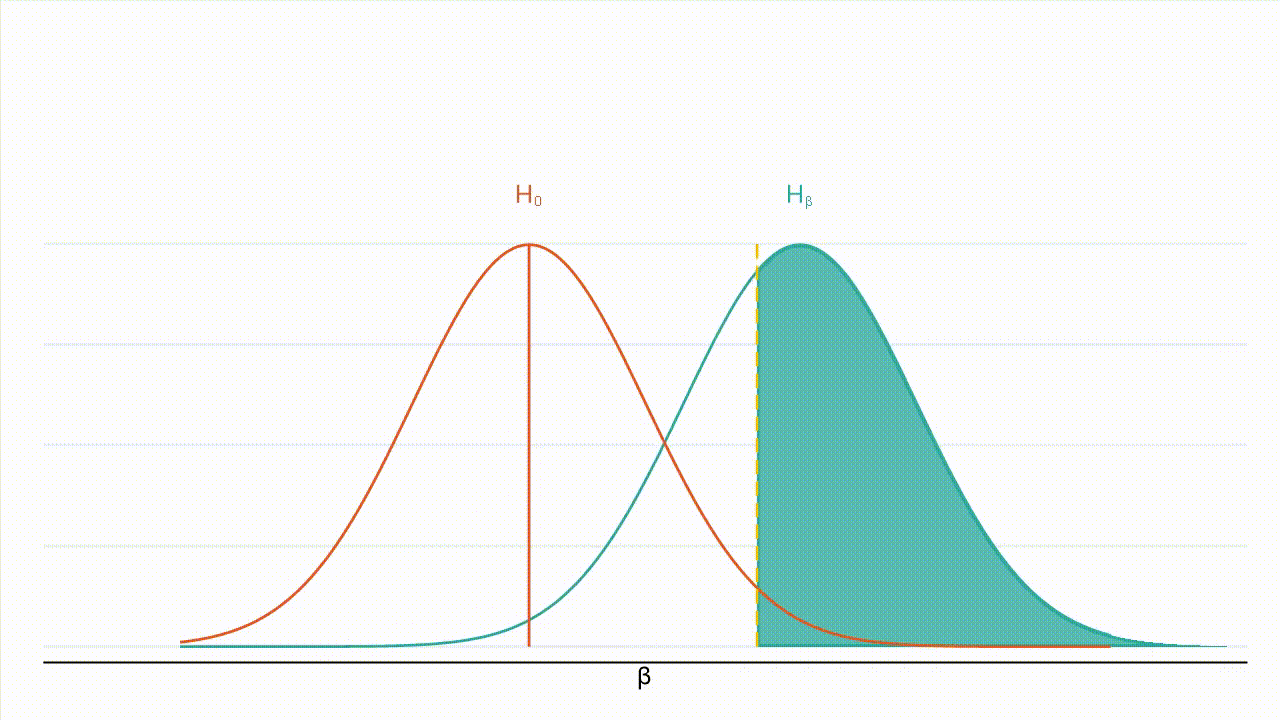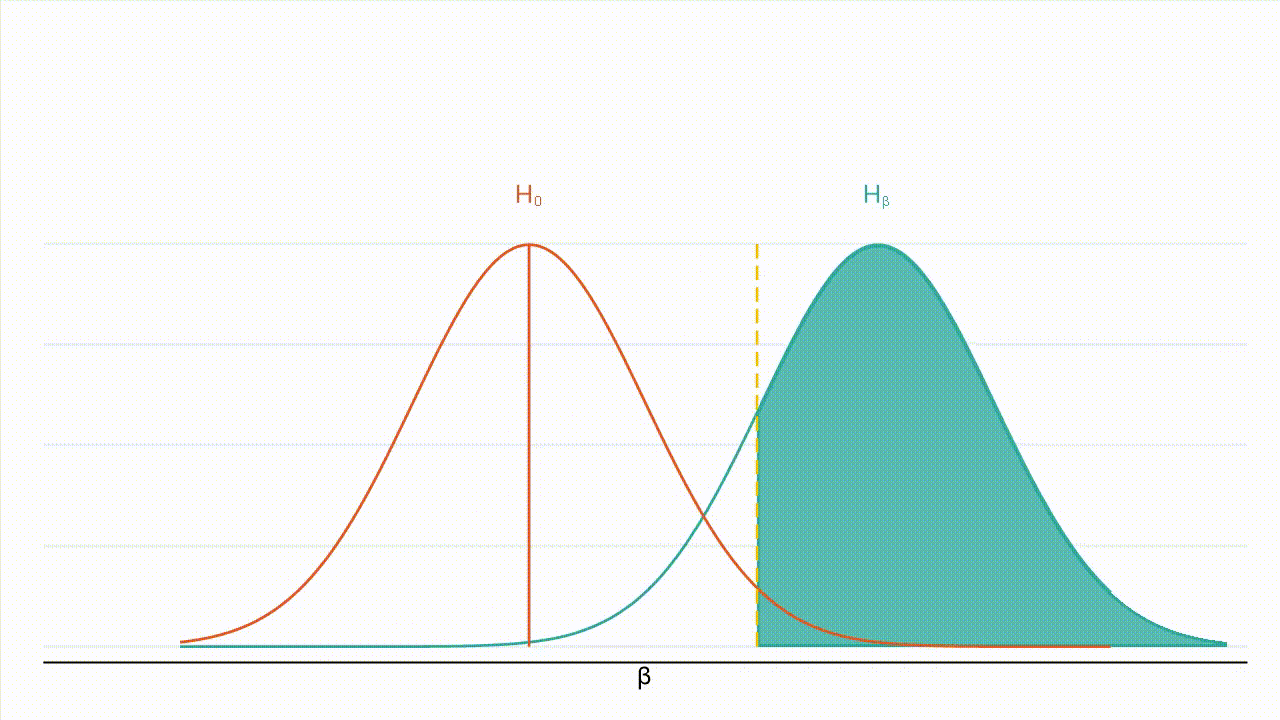
True effect size: Figure 3 : À mesure que la valeur absolue de l’effet réel augmente, la distribution de l’hypothèse alternative se déplace vers la droite et une plus grande part de cette distribution se situe à droite de la valeur critique (la valeur critique étant représentée par la ligne jaune en pointillés et la puissance par la zone ombrée en bleu turquoise).
Allocation du traitement: Comme le montre l’équation 1, l’EMD est minimal lorsque les unités sont réparties de manière égale entre le groupe de traitement et le groupe témoin, c’est-à-dire lorsque P=0,5, tous les autres paramètres restant constants. De façon intuitive, si l’on part d’une allocation inégale du traitement et que l’on ajoute une unité supplémentaire au groupe le moins nombreux (de façon à rendre la répartition moins inégale), les variations d’échantillonnage diminuent davantage que si l’on ajoutait cette même unité au groupe le plus nombreux. Comme la puissance diminue lorsque l’EMD diminue, elle diminue aussi lorsque l’allocation du traitement s’écarte de 0,5. Bien entendu, dans la majorité des cas, les autres paramètres ne sont pas constants. Il arrive parfois qu’il soit préférable de déroger à la répartition 50/50, notamment dans les trois situations suivantes :
- En présence de contraintes budgétaires: Si le coût de l’intervention est élevé et que l’étude est soumise à des contraintes budgétaires, on peut maximiser la puissance statistique en augmentant la taille du groupe témoin (à la fois globalement et en affectant une part plus importante des unités au groupe témoin). Selon Duflo et al. (2007), l’allocation optimale du traitement dans ce type de cas est donnée par :: $\frac{P}{1-P}=\sqrt{\frac{c_c}{c_t}}$ (equation 3)
Où $c_c$ et $c_t$ désignent respectivement le coût par unité du groupe témoin et du groupe de traitement. En d’autres termes, la répartition optimale des unités entre le groupe de traitement et le groupe témoin est proportionnelle à la racine carrée de l’inverse des coûts par unité. Voir la section 6 de McConnell et Hernandez (2015) pour une analyse de l’allocation du traitement en présence de contraintes budgétaires.
- Lorsqu’on s’inquiète de devoir priver certaines personnes d’un programme que l’on pense efficace : Si l’on pense qu’un programme est efficace mais qu’il mérite quand même d’être évalué (par exemple, pour comparer son rapport coût-efficacité avec celui de programmes similaires), on peut opter pour 1) un groupe de traitement plus important ou 2) un modèle d’encouragement, dans le cadre duquel l’ensemble de la population éligible a accès au programme, mais seul le groupe de traitement reçoit des encouragements pour y participer. Pour en savoir plus, consultez la publication de J-PAL Amérique du Nord intitulée Real-world challenges to randomization and their solutions.
- Si les écarts-types sont différents dans le groupe de traitement et dans le groupe témoin suite à l’intervention : Unequal treatment allocation will yield more power if weUne allocation inégale du traitement permet de gagner en puissance statistique si l’on s’attend à ce que le traitement ait un effet sur la variance de la variable d’intérêt. La répartition optimale de l’échantillon correspond alors au rapport entre la variance du groupe de traitement et celle du groupe témoin. Le groupe dont la variance est la plus élevée doit se voir attribuer une plus grande proportion de l’échantillon. Voir McConnell and Vera-Hernandez (2015) et Özler (2021) pour une description du cadre statistique et des calculs de puissance en présence de variances inégales.
Participation, non-conformité et attrition : La non-conformité a pour effet de diluer l’estimation de l’effet du traitement, que ce soit parce que le groupe de traitement contient des unités qui n’ont pas été traitées, parce que le groupe témoin contient des unités qui l’ont été, ou les deux. Il faut donc un échantillon plus important pour détecter l’EMD. Pour reprendre une fois de plus la notation de Duflo et al. (2007) présentée page 33 du randomization toolkit, $c$ désigne la part des unités du groupe de traitement qui reçoivent le traitement et s la part des unités du groupe témoin qui reçoivent le traitement. L’EMD est alors donné par l’équation suivante :
Equation 4: $$ MDE=(t_{1-\kappa}+t_{\frac{\alpha}{2}})\sqrt{\frac{1}{P(1-P)} \times \frac{\sigma^2}{N}} \times \frac{1}{c-s} $$Lorsque le taux de participation n’est pas de 100 % ou en cas de non-conformité, la taille d’échantillon nécessaire est inversement proportionnelle à $(c-s)$, i.e., , c’est-à-dire à la différence de participation entre le groupe de traitement et le groupe témoin. Par exemple, si seule la moitié du groupe de traitement participe au traitement, et que personne n’y participe dans le groupe témoin (donc si (i.e., $c-s=0.5$), et toutes choses égales par ailleurs, la taille d’échantillon nécessaire pour détecter une taille d’effet donnée sera quatre fois plus grande que dans une situation de conformité parfaite.
Dans la mesure où l’attrition diminue la taille de l’échantillon, elle peut également réduire la puissance statistique (ou, à l’inverse, faire augmenter l’EMD). Des taux d’attrition différents dans le groupe de traitement et le groupe témoin peuvent également rapprocher ou éloigner le ratio d’allocation de l’allocation initiale du traitement. Rickles et al. (2019) expliquent comment différents types d’attrition (aléatoire, conditionnelle à l’assignation du traitement ou conditionnelle aux covariables) peuvent affecter l’EMD.
Relation entre l’EMD et les paramètres qui influencent la puissance statistique D’un point de vue théorique, les paramètres mentionnés ci-dessus affectent l’EMD de la même manière qu’ils affectent la puissance statistique, comme le montre le tableau 1 présenté plus bas.
Randomisation en grappes
Les calculs de puissance présentés jusqu’à présent concernaient la randomisation au niveau de l’unité d’observation. Pour les protocoles de randomisation en grappes, où chaque unité de randomisation contient plusieurs unités d’observation, les équations utilisées pour effectuer ces calculs doivent être modifiées. Un modèle en grappes consiste par exemple à randomiser des ménages tout en mesurant les résultats au niveau individuel, ou bien à randomiser des cliniques en mesurant les résultats au niveau des patients. Au sein d’une même grappe, les unités ont tendance à se comporter de manière similaire. Par exemple, les membres d’un même ménage sont susceptibles de voter de la même manière, les patients d’une même clinique ont des chances de vivre dans le même quartier ou de recevoir le même type de soins, etc. Ce constat a des implications en termes de puissance : de façon intuitive, les variables de résultat au sein d’une même grappe étant corrélées, il y a plus de risques pour qu’un changement observé au niveau des variables de résultat soit attribué à tort au traitement plutôt qu’à un autre bouleversement ayant affecté l’ensemble de la grappe (Duflo et al., 2007). Par conséquent, si toute augmentation de N accroît la puissance statistique, cette augmentation est généralement plus importante si elle résulte de l’ajout de grappes supplémentaires (k) plutôt que de l’ajout d’unités supplémentaires dans une grappe existante (m). Toutes choses égales par ailleurs, l’ajout de nouvelles grappes augmente davantage la puissance que l’ajout d’unités supplémentaires à chaque grappe.
Coefficient de corrélation intra-grappe
La corrélation entre les unités d’une même grappe est exprimée par le coefficient de corrélation intra-grappe (CCI, ou ICC en anglais). En termes formels, ce coefficient correspond à la proportion de la variance totale de la variable d’intérêt qui est due à la variance entre les grappes (Gelman et Hill, 2006) :
Equation 5:$ICC = \frac{\sigma^2_{between-cluster}}{\sigma^2_{between-cluster}+\sigma^2_{within-cluster}}$
Si les individus au sein d’une même grappe étaient tous identiques (par exemple, si tous les membres d’un même ménage votaient exactement de la même façon), les variations au sein de l’échantillon seraient exclusivement dues aux différences entre les grappes plutôt qu’aux différences entre individus d’une même grappe. Dans ce cas, le CCI serait égal à 1 et la taille effective de l’échantillon correspondrait au nombre de grappes. Si, en revanche, les individus d’une même grappe étaient complètement indépendants les uns des autres, le CCI serait égal à 0. Dans ce cas, la taille effective de l’échantillon correspondrait au nombre d’individus.
Dans la pratique, le CCI se situe généralement entre 0 et 1, ce qui signifie que la taille effective de l’échantillon est supérieure au nombre de grappes, mais inférieure au nombre d’unités individuelles. La valeur réelle du CCI dépend du degré de similitude entre les unités d’une même grappe : plus ces dernières se comportent de façon similaire, plus la valeur du CCI augmente (et plus la taille effective de l’échantillon diminue). Cette réduction de la taille effective de l’échantillon limite à son tour le degré de précision des estimations et augmente l’EMD. Vous trouverez des conseils pour calculer le CCI dans la section "Conseils pratiques", plus bas dans cette ressource.
Équations de puissance pour les modèles en grappes
Comme mentionné précédemment, dans les modèles en grappes, la taille totale de l'échantillon $N$ peut être divisée en le nombre de grappes $k$ et le nombre moyen d'unités par grappe $m$. Pour ajuster la corrélation au sein des grappes, les calculs de puissance pour les modèles en grappes incluent l'effet de plan, qui est donné par $(1+(m-1) \times ICC)$. L'équation pour l'EMD dans un modèle en grappes est donnée par :
Equation 6: $$ MDE = (t_{1-\kappa}+t_{\frac{\alpha}{2}}) \sqrt{\frac{1}{P(1-P)} \times \frac{\sigma^2}{N} \times (1+(m-1)\times ICC)} $$À l'exception de $N$ (pour les raisons décrites précédemment), les composantes de cette équation affectent l'EMD de manière similaire à ce qui a été décrit plus haut pour une randomisation au niveau individuel. Notez ici qu'une augmentation du coefficient de corrélation intraclasse (CCI) entraîne une augmentation de l'EMD ou de la taille d'échantillon requise. Par exemple, en gardant $N$ et $P$ constants, en fixant $m=50$, et avec un CCI de 0,07, l'erreur-type de l'estimateur de l'effet du traitement (le terme de la racine carrée) double. En conséquence, l'EMD double, tandis que la taille d'échantillon nécessaire quadruple.
Conseils pratiques
Cette section passe en revue les différentes sources d’informations sur chacun des paramètres intervenant dans les calculs de puissance et donne des conseils pour exploiter les résultats de ces calculs.
Rassembler les informations nécessaires
Certains des paramètres qui interviennent dans les calculs de puissance reposent sur des décisions ou des hypothèses formulées par le chercheur et son partenaire, tandis que d’autres sont calculés à partir de données existantes.
Paramètres basés sur des décisions ou des hypothèses :
- La puissance, (1-κ), est généralement fixée à 80 %, ou 0,8, même s’il arrive aussi qu’elle soit fixée à 90 %. S’il peut être tentant d’augmenter la puissance de l’étude, il faut savoir que cela augmente aussi le risque de faux positif (erreur de type I). Pour plus d’informations, voir Cohen (1988).
- Le niveau de signification, α, est généralement fixé à 5 %, c’est-à-dire α=0,05.
- Les unités de randomisation et d’observation : Les unités de randomisation et d’observation ne sont pas obligatoirement les mêmes. Voir la section « Mise en œuvre » de la ressource sur la randomisation pour plus d’informations sur la définition de ces deux éléments. Dans le cas des modèles en grappes, si l’ajout de grappes supplémentaires permet généralement d’augmenter davantage la puissance que l’ajout d’unités supplémentaires aux grappes existantes, la première solution est souvent plus coûteuse à mettre en œuvre.
- L’EMD peut être choisi parce qu’il présente un intérêt pratique, par exemple parce qu’il s’agit de l’effet minimum qui justifierait l’investissement du partenaire de mise en œuvre dans le programme, ou qui le convaincrait de déployer le programme à grande échelle. Notez que les articles publiés qui portent sur des évaluations d’interventions similaires tendent à fournir une estimation optimiste de la taille d’effet qu’il est raisonnable d’attendre. De plus, comme l’estimation de l’effet risque ensuite d’être affaiblie par le phénomène de non-conformité, l’ampleur de l’effet escompté doit être ajustée pour tenir compte du taux de conformité attendu dans les deux groupes.
- Si vous ne trouvez aucune information concernant la taille d’effet à laquelle on peut raisonnablement s’attendre, Cohen (1988) propose des règles empiriques reposant sur les écarts-types4 : 0,2 écart-type pour un petit EMD, 0,5 écart-type pour un EMD moyen et 0,8 écart-type pour un EMD important. Ces valeurs sont cependant basées sur des expérimentations de psychologie sociale menées en laboratoire auprès d’étudiants de premier cycle, et il a depuis été affirmé qu’il n’était pas réaliste de les appliquer aux situations réelles rencontrées dans certains secteurs et régions. Voir par exemple Kraft (2019) (article de blog correspondant) et Evans et Yuan (2020) (article de blog correspondant) pour savoir pourquoi il semble plus réaliste de choisir un EMD plus petit pour les interventions dans le domaine de l’éducation.
- Une autre option consiste à déterminer la taille de l’échantillon, N, en fonction du budget de l’étude ou des contraintes du partenaire (par exemple, le nombre d’élèves éligibles dans les écoles du partenaire, le nombre de dispensaires dans le district, etc.).
- Le nombre de grappes (k) et la taille de chaque grappe (m) : En raison de contraintes logistiques (transport, frais de personnel, etc.), il est généralement moins coûteux d’interroger une personne supplémentaire au sein d’une grappe existante que d’ajouter une nouvelle grappe. Toutefois, le coût marginal décroissant qui résulte de l’ajout d’une unité supplémentaire à une grappe existante doit être mise en balance avec la puissance marginale décroissante engendrée par l’ajout de chaque unité supplémentaire. Le nombre optimal de grappes et d’unités au sein de ces grappes varie également en fonction du CCI attendu.
- L’allocation du traitement, P, peut être manipulée de façon à maximiser la puissance ou à minimiser les coûts. Comme indiqué plus haut, la puissance est généralement maximale lorsque les unités sont réparties de manière égale entre le groupe de traitement et le groupe témoin, mais plus le nombre d’unités à traiter est important, plus les coûts sont élevés. Une allocation inégale du traitement (par exemple 30 % dans le groupe de traitement et 70 % dans le groupe témoin) au sein d’un échantillon global de plus grande taille peut donc permettre d’obtenir une puissance statistique plus grande qu’une répartition 50/50 au sein d’un échantillon plus petit. Il peut être intéressant de tester différentes tailles d’échantillon et différentes allocations en tenant compte des contraintes budgétaires afin de trouver le modèle qui permet de maximiser la puissance de l’étude. Voir le chapitre 6 de Running Randomized Evaluations pour un guide sur l’adaptation du ratio d’allocation à différents scénarios concrets.
Paramètres calculés à partir de données issues de l’enquête initiale, du projet pilote ou d’autres études existantes, ou de données accessibles au public :
- La variance des variables d’intérêt (𝞼2) doit idéalement se trouver dans les données de l’enquête initiale. Si ce n’est pas le cas, on peut éventuellement la calculer à partir d’autres données portant sur la même population de référence ou sur une population similaire, ou la trouver dans des articles sur des études portant sur des sujets similaires, de préférence menées auprès de populations comparables. Parmi les sources de données utiles, citons notamment le Dataverse de J-PAL/IPA, les données administratives, les données du programme d’études sur la mesure du niveau de vie (LSMS), etc5. Notons que la variance est généralement supposée égale dans les différents bras de traitement.
- CCI : De la même manière, le CCI peut être estimé à partir des données de l’enquête initiale ou d’autres données issues d’enquêtes et d’articles portant de préférence sur la même population ou sur une population similaire. McKenzie (2012) explique l’une des méthodes de calcul du CCI à partir des données de l’enquête initiale avec Stata.
- Participation, non-conformité et attrition : Consultez la littérature portant sur des programmes similaires à l’intervention étudiée pour vous faire une idée approximative du taux de participation auquel vous pouvez raisonnablement vous attendre. Ne vous limitez pas aux articles universitaires : il est possible de trouver des informations pertinentes dans des documents relevant aussi bien de la littérature publiée que de la littérature grise, des rapports, etc.
Calculs initiaux
Les calculs initiaux doivent se concentrer sur la faisabilité de l’étude. Une fois que le projet envisagé aura passé avec succès un test élémentaire de faisabilité, les calculs de puissance pourront être affinés et actualisés à l’aide de nouvelles données.
Lorsque vous effectuez vos premiers calculs, il est important de garder à l’esprit les points suivants :
- Utilisez les meilleures données parmi celles auxquelles vous avez facilement accès. Évitez de vous perdre dans des démarches sans fin pour tenter d’accéder à des données non publiques ou de régler des détails qui pourront être corrigés par la suite.
- Pour faire des calculs de puissance, vous n’avez pas forcément besoin de trouver des données pour chaque paramètre. Effectuez une analyse de sensibilité (voir ci-dessous) pour identifier les paramètres qui ont le plus d’impact sur la puissance. Votre équipe pourra alors concentrer ses efforts sur la recherche d’estimations fiables pour les paramètres les plus importants.
- De même, s’il vous manque des informations sur certains déterminants de la puissance statistique, formulez des hypothèses plausibles pour vérifier la faisabilité potentielle de l’étude. Par exemple, pour estimer les tailles d’effet, utilisez les règles empiriques mentionnées plus haut, selon lesquelles une augmentation de 0,2 écart-type correspond à un effet de petite taille. Prenez cette valeur comme EMD de départ et calculez la taille d’échantillon nécessaire pour obtenir une première idée de la faisabilité de l’étude.
- Réalisez une analyse de sensibilité pour voir comment la puissance statistique varie lorsque la valeur des différents paramètres clés est modifiée. Concentrez-vous en particulier sur :
- Les hypothèses clés comme l’effet minimum, le taux de participation et la corrélation intra-grappe. Faites preuve de réalisme, voire d’un pessimisme excessif, en ce qui concerne le taux de participation.
- Toute information ayant fait l’objet d’une hypothèse par manque de données (comme les tailles d’effet dans le point ci-dessus).
- Les domaines dans lesquels vous disposez d’une certaine marge de manœuvre pour ajuster le protocole, par exemple en ajoutant des unités supplémentaires aux grappes plutôt que l’inverse, en modifiant l’allocation du traitement, etc.
- Pour effectuer vos calculs, envisagez aussi bien les méthodes d’analyse que les méthodes de simulation. Les méthodes de simulation sont particulièrement utiles pour les protocoles de recherche les plus complexes (McConnell et Vera-Hernandez, 2015). Ces méthodes consistent à : 1) générer un faux ensemble de données comprenant une taille d’effet et un protocole prédéfinis, 2) tester l’hypothèse nulle, 3) répéter les étapes 1 et 2 un très grand nombre de fois (généralement 1 000 ou plus), et 4) diviser le nombre total de rejets obtenus à l’étape 2 par le nombre total de tests effectués afin de calculer la puissance de l’étude. Si l’on dispose de données de qualité sur la population étudiée, ces méthodes peuvent également être utilisées pour calculer des intervalles de confiance simulés pour l’hypothèse nulle, ou pour effectuer des calculs de puissance pour un échantillon de petite taille au sein duquel certaines des hypothèses paramétriques concernant les distributions de probabilités sont susceptibles de ne pas être satisfaites. Des exemples de code pour ces deux approches sont disponibles sur notre GitHub.
Affiner les calculs
Si les calculs initiaux indiquent que l’étude semble faisable, les étapes suivantes consistent à tester de façon itérative les détails du protocole expérimental et à affiner les calculs afin d’obtenir une estimation plus précise de la taille d’échantillon nécessaire. Notez que les calculs ne nécessitent parfois que des ajustements mineurs, voire aucun ajustement. Par exemple, il n’est pas forcément nécessaire de faire davantage de tests si la taille de l’échantillon est pré-déterminée et que les calculs initiaux effectués à partir de données fiables et pertinentes ont montré que le protocole permettait d’atteindre une puissance satisfaisante pour un large éventail d’hypothèses concernant le CCI, le taux de participation, etc. En revanche, affiner les calculs peut s’avérer particulièrement utile dans deux situations clés :
- Si le protocole a subi des changements importants depuis la réalisation des calculs initiaux, par exemple si vous avez modifié le nombre de bras de traitement, la procédure d’admission (ce qui peut affecter la participation), l’unité de randomisation, ou encore si vous avez décidé de mesurer les effets sur des sous-groupes particuliers. De telles modifications doivent être prises en compte dans les estimations de la puissance statistique.
- Si vous obtenez de meilleures estimations des paramètres clés. Si l’étude a passé avec succès un test initial de faisabilité, mais que vous n’aviez pas réussi à trouver des estimations satisfaisantes de certains paramètres fondamentaux pour vos calculs de puissance initiaux, il peut être utile de chercher des données supplémentaires afin d’affiner votre estimation de la puissance. Vous pouvez notamment demander à votre partenaire de vous fournir des données opérationnelles détaillées, ou demander à une entité tierce de vous fournir des données administratives ou des données d’enquête non publiques.
Par ailleurs, il existe également d’autres éléments du protocole qui, s’ils n’ont pas été intégrés aux calculs initiaux, doivent être pris en compte à ce stade pour affiner les calculs. Vous en trouverez une description ci-dessous.
Autres éléments du protocole à prendre en compte
Variables de résultat binaires : La variable d’intérêt peut être une variable binaire, comme le fait d’avoir ou non un emploi à l’issue d’un programme de formation professionnelle, de passer ou non dans la classe supérieure à l’issue d’un programme de tutorat, etc. Si l’intuition qui sous-tend le calcul de l’EMD et de la taille de l’échantillon est la même que pour une variable continue, la taille de l’effet et la variance de la variable d’intérêt changent selon la nature (logarithme de l’odds ratio ou différence de probabilité) et la méthode de calcul (régression logistique ou linéaire) de l’effet. Voir la section 5 de McConnell et Vera-Hernandez (2015) pour une représentation statistique de la puissance et un exemple de code pour les variables de résultat binaire.
Grappes de taille inégale : Il arrive souvent que les grappes soient de taille inégale du fait des contraintes pratiques qui pèsent sur la répartition des unités. Cela peut se traduire par un nombre inégal de grappes au sein de chaque groupe expérimental ou par un nombre inégal d’unités au sein des grappes. Par exemple, une étude randomisée au niveau de l’enseignant mais qui mesure les résultats au niveau des élèves aura probablement des grappes de tailles différentes. À moins que la taille des grappes ne varie fortement, la taille totale de l’échantillon requis en présence de grappes inégales ne sera que légèrement supérieure à celle requise pour des grappes de taille égale. Pour plus d’informations, voir la page 12 de McConnell et Vera-Hernandez (2015).
Randomisation stratifiée : Bien que la randomisation ait pour effet d’éliminer tout biais systématique entre le groupe de traitement et le groupe témoin ex ante, les chercheurs peuvent choisir de stratifier l’assignation aléatoire afin de s’assurer que le groupe de traitement et le groupe témoin comptent une même proportion d’unités présentant une ou plusieurs caractéristique(s) importante(s). Dans la mesure où la variable de stratification a des chances d’être corrélée avec la variable de résultat, la stratification réduit généralement la variance résiduelle de la variable de résultat, ce qui augmente la puissance de l’étude. Pour plus d’informations sur la stratification, voir la ressource de J-PAL consacrée à la randomisation et Athey et Imbens (2016).
Hétérogénéité des effets du traitement : La stratification peut également être utile pour mesurer l’hétérogénéité des effets du traitement dans différents sous-groupes. On peut par exemple trouver intéressant de comparer les résultats des hommes et des femmes, des électeurs ayant fait des études supérieures et de ceux qui n’en ont pas fait, et ainsi de suite. Si c’est le cas, il est utile d’effectuer des calculs de puissance distincts pour les deux groupes concernés afin de s’assurer que l’étude a une puissance suffisante pour détecter les effets hétérogènes qui vous intéressent.
Ajout de covariables : La même logique que pour la stratification s’applique ici : grâce à la randomisation, il n’est pas indispensable d’inclure des covariables pour obtenir une estimation non biaisée de l’effet du traitement, mais il peut être utile de le faire malgré tout pour limiter la variance résiduelle de la variable de résultat. Toutes choses égales par ailleurs, cette démarche augmente la puissance, même si l’ampleur de cette augmentation dépend de la taille du jeu de données et de la corrélation entre les covariables et la variable de résultat, entre autres facteurs6. Consultez la ressource sur l’analyse des données pour des conseils sur l’inclusion de covariables dans votre analyse, et Athey & Imbens (2016) pour plus d’informations.
Bras de traitement multiples : Si le protocole de l’étude comporte plusieurs bras, on peut trouver intéressant d’effectuer des comparaisons par paire entre les différents bras de traitement, ou entre un bras de traitement et le groupe témoin. Veillez à ce que l’étude bénéficie de la puissance nécessaire pour détecter l’EMD le plus faible parmi les différentes comparaisons prévues (cela peut toutefois entraîner une hausse significative des coûts si l’on compare deux traitements similaires). On peut commencer par calculer l’EMD pour chaque comparaison par paire en supposant une répartition égale des unités, puis recalculer l’EMD pour différentes configurations de l’échantillon, afin de déterminer quelles comparaisons il est réaliste d’effectuer compte tenu des contraintes budgétaires. Notez que si, lors de l'analyse, vous prévoyez d'ajuster les comparaisons multiples entre les groupes (par exemple, témoin et traitement 1, témoin et traitement 2, traitements 1 et 2, etc.), vous devez en faire autant dans vos calculs de puissance.
Variables d’intérêt multiples : Comme dans le cas des traitements multiples, si l’étude examine plusieurs variables d’intérêt, il est important de s’assurer qu’elle a la puissance nécessaire pour chacune de ces variables. En d’autres termes, il faut choisir la taille d’échantillon et le protocole qui permettront de détecter l’EMD le plus faible parmi toutes les variables étudiées.
Hypothèses multiples : Lorsqu’on teste des hypothèses multiples, il est important de noter que le niveau de signification ou la probabilité de rejeter l’hypothèse nulle augmente avec le nombre d’hypothèses. Pour remédier à ce problème, on peut appliquer une procédure de correction des tests multiples, comme les corrections de Bonferroni ou de Benjamini Hochberg. La puissance peut augmenter ou diminuer selon le type de correction, le nombre d’hypothèses et la corrélation entre les hypothèses nulles (Porter 2016 ; McConnell et Vera-Hernandez 2015), mais si vous prévoyez d’appliquer ces méthodes de correction dans l’analyse, il est important de le faire aussi dans les calculs de puissance afin de vous assurer que votre étude bénéficie d’une puissance suffisante. Voir la ressource de J-PAL sur l’analyse des données, le guide des méthodes d’EGAP et McKenzie (2020) pour une description plus approfondie du problème, la section 4 de List, Shaikh et Xu (2016) pour une démonstration des méthodes de correction de tests multiples en présence de plusieurs bras de traitement et d’effets hétérogènes, et les pages 29-30 de McConnell et Vera-Hernandez (2015) pour une description des applications aux calculs de puissance
Exploiter les résultats des calculs de puissance
Interpréter l’EMD calculé
Pour une variable d’intérêt continue, l’effet minimum se mesure dans la même unité que la variable en question, à moins qu’il ne s’agisse d’une taille d’effet standardisée (la taille d’effet étant divisée par l’écart-type de la variable d’intérêt). Dans ce cas, l’EMD est exprimé en termes d’écart-type. Pour ce faire, il suffit de réarranger le terme de la variance dans l’équation 1.
Si la variable d’intérêt est une variable binaire, on mesure la taille d’effet en calculant la différence entre le logarithme de l’odds ratio ou la probabilité de succès du groupe de traitement et celui ou celle du groupe témoin. Dans le second cas, l’EMD est exprimé en points de pourcentage (par exemple, un EMD de 0,06 est interprété comme une augmentation de 6 points de pourcentage par rapport à la moyenne du groupe témoin). Notez que la commande Stata power permet de calculer cette seconde mesure (probabilité de succès).
Il est important de garder à l’esprit que les calculs de puissance statistique sont basés sur la distribution d’échantillonnage sous-jacente de l’effet estimé. Ainsi, même si l’étude a une puissance de 80 %, il y a toujours 20 % de chances de ne détecter aucun effet alors que le programme en a un. À l’inverse, il est possible qu’une étude dont la puissance est insuffisante parvienne tout de même à détecter un effet réel, même si la probabilité pour qu’elle le fasse est plus faible. La section suivante aborde les ajustements que l’on peut envisager d’effectuer si l’étude manque de puissance.
Résolution de problèmes : les protocoles à faible puissance
Si l’étude n'est pas assez puissante mais néanmoins réalisable, vous pouvez essayer d’en ajuster le protocole ou d’augmenter la taille de l’échantillon. Voici quelques idées :
- Si le budget est la principale contrainte : Envisagez de ne pas faire d’enquête initiale (McKenzie 2012), de modifier l’allocation du traitement (en ajoutant des unités au groupe témoin et en réduisant le nombre d’unités dans le groupe de traitement), d’ajouter des unités plutôt que des grappes, ou de simplifier le protocole (par exemple, en supprimant un bras de traitement, en limitant le nombre de comparaisons par paires de traitements similaires, etc.). Pour un cadre statistique et un exemple de code de simulation permettant d’optimiser les coûts, voir la discussion qui débute page 21 de McConnell et Vera-Hernandez (2015).
- Notons que la stratification a un effet ambigu sur la puissance. Comme indiqué plus haut, l’ajout de covariables ou la stratification augmentent la précision des estimations de l’effet du traitement, réduisant ainsi la taille totale de l’échantillon nécessaire. Cependant, il y a de fortes chances pour que la taille d’échantillon nécessaire pour détecter une hétérogénéité des effets entre les strates soit plus importante. Si le budget est limité, il peut donc être utile de tester l’impact de la stratification sur la puissance de l’étude.
- Si la taille de l’échantillon est la principale contrainte : Une option évidente consiste à simplifier le protocole, par exemple en réduisant le nombre de bras de traitement ou en limitant le nombre de variables d’intérêt principales pour ne retenir que les plus importantes. Comme mentionné plus haut, l’inclusion de covariables peut augmenter la puissance de l’étude, mais si la taille de l’échantillon est fixe et constitue le principal facteur limitant, il est peu probable que vous soyez en mesure de détecter des effets de traitement hétérogènes. Une autre solution, si le budget le permet, consiste à augmenter le nombre de vagues de collecte de données (McKenzie, 2012).
Si, même en procédant à tous les ajustements possibles du protocole, l’étude reste trop peu puissante, les risques liés à la poursuite de l’étude l’emportent sur ses avantages, et il convient alors de suspendre les travaux en attendant de pouvoir augmenter la taille de l’échantillon, de disposer de données supplémentaires ou autre pour poursuivre. Une étude qui manque de puissance est, au mieux, une perte d’argent, car elle ne permettra pas de déterminer si le programme est efficace. Dans le pire des cas, des résultats nuls obtenus par une étude trop peu puissante peuvent être utilisés pour justifier l’arrêt du programme si les décideurs prennent ces résultats pour preuve de l’inefficacité du programme lui-même. Pour en savoir plus, consultez le guide de J-PAL Amérique du Nord à ce sujet
Exemple de code
See our GitHub page for sample Stata and R code for conducting power calculations using built-in commands and by simulation.
Dernière modification : août 2021.
Ces ressources sont le fruit d’un travail collaboratif. Si vous constatez un dysfonctionnement, ou si vous souhaitez suggérer l'ajout de nouveaux contenus, veuillez remplir ce formulaire.
Ce document a été traduit de l’anglais par Marion Beaujard.
Nous remercions WIlliam Parienté pour ses commentaires précieux. Ce document a été traduit de l’anglais par Marion Beaujard. Toute erreur est de notre fait.
In the case of a binary outcome variable, the variance is a function of the mean of the variable. For a given binary variable $Y$ which takes values 0 or 1 and has mean $P$, $var(Y) = (1-P) \times $P$. The variance for the control and the treatment groups are likely to be different after the intervention since the treatment mean is likely to change after the intervention.
Additional Resources
McConnell, Brendon, and Marcos Vera-Hernandez. 2015. "Going beyond simple sample size calculations: a practitioner's guide." IFS Working Paper W15/17. https://ifs.org.uk/publications/7844.
Kondylis, Florence, and John Loeser. Power Dashboard: Cash transfer size, nonlinearities, and benchmarking. Associated blog posts: part 1 and part 2.
Rickles, Jordan, Kristina Zeiser, and Benjamin West. 2019. "Accounting for Student Attrition in Power Calculations: Benchmarks and Guidance." Journal of Research on Educational Effectiveness, 11(4): 622-644. https://doi.org/10.1080/19345747.2018.1502384.
Evidence in Governance and Politics (EGAP)'s multiple hypotheses guide.
References
Athey, Susan, and Guido Imbens. 2017. “The Econometrics of Randomized Experiments.” Handbook of Field Experiments, 73-140. doi:10.1016/bs.hefe.2016.10.003.
Baird, Sarah, J. Aislinn Bohren, Craig Mcintosh, and Berk Ozler. 2018. “Optimal Design of Experiments in the Presence of Interference.” The Review of Economics and Statistics, 100(5): 844-860. https://doi.org/10.1162/rest_a_00716
Cohen, Jacob. 1998. Statistical Power Analysis for the Behavioral Sciences. 2nd ed., Routledge: New York, USA. https://doi.org/10.4324/9780203771587.
Duflo, Esther, Rachel Glennerster, and Michael Kremer. 2007. “Using Randomization in Development Economics Research: A Toolkit.” Handbook of Development Economics, 3895-3962. doi:10.1016/s1573-4471(07)04061-2.
Evans, David. "We Need Interventions that Improve Student Learning. But How Big is a Big Impact?" Center for Global Development (blog), August 26, 2019. https://www.cgdev.org/blog/we-need-interventions-improve-student-learning-how-big-big-impact. Last accessed August 3, 2021.
Evans, David, and Fei Yuan. 2020. "How Big Are Effect Sizes in International Education Studies?" Center for Global Development Working Paper 545. https://www.cgdev.org/sites/default/files/how-big-are-effect-sizes-international-education-studies.pdf.
Evans, David, and Fei Yuan. 2020. "How Big Are Effect Sizes in International Education Studies?" Center for Global Development (blog), August 27, 2020. https://www.cgdev.org/blog/how-big-are-impacts-international-education-interventions. Last accessed August 3, 2021.
Fisher, Ronald. 1935. The Design of Experiments. Oliver and Boyd: Edinburgh, UK.
Gelman, Andrew, and Jennifer Hill. 2006. "Sample size and power calculations" in Data Analysis Using Regression and Multilevel/Hierarchical Models, 437-454. Cambridge University Press: Cambridge, UK. https://www.cambridge.org/highereducation/books/data-analysis-using-regression-and-multilevel-hierarchical-models/32A29531C7FD730C3A68951A17C9D983?utm_campaign=shareaholic&utm_medium=copy_link&utm_source=bookmark.
Kraft, Matthew A. 2020. "Interpreting Effect Sizes of Education Interventions." Educational Researcher, 49(4): 241-253. https://doi.org/10.3102/0013189X20912798.
List, John A., Azeem M. Shaikh, and Yang Xu. 2019. "Multiple hypothesis testing in experimental economics." Experimental Economics, 22: 773-793. https://doi.org/10.1007/s10683-018-09597-5.
Liu, Xiaofeng. 2013. Statistical Power Analysis for the Social and Behavioral Sciences: Basic and advanced techniques. Routledge: New York, USA. https://doi.org/10.4324/9780203127698.
McConnell, Brendon, and Marcos Vera-Hernandez. 2015. "Going beyond simple sample size calculations: a practitioner's guide." IFS Working Paper W15/17. https://ifs.org.uk/publications/7844.
McKenzie, David. "An overview of multiple hypothesis testing commands in Stata." World Bank Development Impact (blog), June 1, 2021. https://blogs.worldbank.org/impactevaluations/overview-multiple-hypothesis-testing-commands-stata. Last accessed August 3, 2021.
McKenzie, David. 2012. "Beyond baseline and follow-up: The case for more T in experiments." Journal of Development Economics, 99(2): 210-221. https://openknowledge.worldbank.org/bitstream/handle/10986/3403/WPS5639.pdf?sequence=1&isAllowed=y.
McKenzie, David. "Power Calculations 101: Dealing with Incomplete Take-up." World Bank Development Impact (blog), May 23, 2011. https://blogs.worldbank.org/impactevaluations/power-calculations-101-dealing-with-incomplete-take-up. Last accessed August 3, 2021.
McKenzie, David. "Tools of the Trade: Intra-cluster correlations." World Bank Development Impact (blog), December 02, 2012. https://blogs.worldbank.org/impactevaluations/tools-of-the-trade-intra-cluster-correlations. Last accessed August 3, 2021.
Özler, Berk. "When should you assign more units to a study arm?" World Bank Development Impact (blog), June 21, 2021. https://blogs.worldbank.org/impactevaluations/when-should-you-assign-more-units-study-arm?CID=WBW_AL_BlogNotification_EN_EXT. Last accessed August 3, 2021.
Porter, Kristin E. 2016. "Statistical Power in Evaluations That Investigate Effects on Multiple Outcomes: A Guide for Researchers." MDRC Working Paper. https://www.mdrc.org/sites/default/files/EC%20Methods%20Paper_2016.pdf.
Rickles, Jordan, Kristina Zeiser, and Benjamin West. 2019. "Accounting for Student Attrition in Power Calculations: Benchmarks and Guidance." Journal of Research on Educational Effectiveness, 11(4): 622-644. https://doi.org/10.1080/19345747.2018.1502384.